Why Does RSA Actually Work?

March 23, 2023 by patrickd

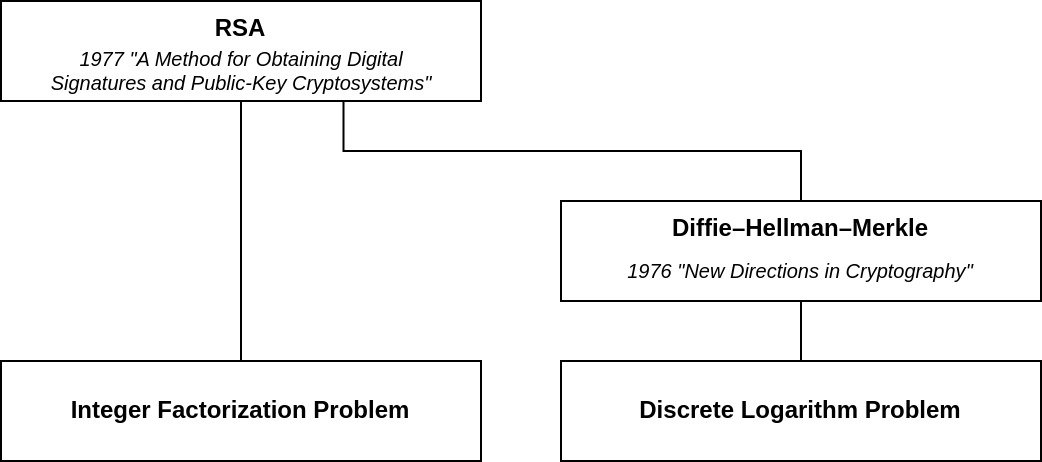
RSA encryption appears so incredibly elegant and simple, it's as if it were some sort of mathematical magic. This article is an attempt to give the reader some intuition about why it works and make the seemingly magical aspects graspable. Note that it avoids mathematical proves where possible, it does not attempt to give an explanation on how to implement RSA securely or efficiently, and it skips any concepts that have been deemed irrelevant for understanding the "why".

The Magic

${p}$ and ${q}$ chosen as large random prime numbers

${N}={p}\cdot{q}$

$\phi{\left({N}\right)}=\phi{\left({p}\right)}\cdot\phi{\left({q}\right)}={\left({p}-{1}\right)}\cdot{\left({q}-{1}\right)}$, phi being "Euler's Totient Function"

${e}={65537}$, fullfills requirements of ${1}<{e}<\phi{\left({n}\right)}$ and ${\gcd{{\left({e},\phi{\left({n}\right)}\right)}}}={1}$, combined with ${N}$ makes up the public key ${K}{\left({e},{N}\right)}$

${d}\equiv{e}^{{-{1}}}\ \text{ mod }\ \phi{\left({N}\right)}$, combined with ${N}$ makes up the private key ${k}{\left({d},{N}\right)}$

${c}\equiv{m}^{{e}}\ \text{ mod }\ {N}$, is the encrypted ciphertext ${c}$ of the message ${m}$

${m}\equiv{c}^{{d}}\ \text{ mod }\ {N}$, is the decrypted message ${m}$ from the ciphertext ${c}$

What is $\equiv\text{mod}$ ?

You might already know that the triple line equal sign $\equiv$ stands for "congruence" rather than "equality" while $\text{mod}$ is short for modulo which yields the remainder of a division operation.

In congruence both sides have the same remainder when divided by a particular modulus.

${\left({a}\equiv{b}\ \text{ mod }\ {n}\right)}\Leftrightarrow{\left({b}\equiv{a}\ \text{ mod }\ {n}\right)}$

${a}\ \text{ mod }\ {n}={b}\ \text{ mod }\ {n}$

Example

${\left({2}\ \text{ mod }\ {5}={2}\right)}$ and ${\left({12}\ \text{ mod }\ {5}={2}\right)}$

therefore

${\left({2}\equiv{12}\ \text{ mod }\ {5}\right)}$ and ${\left({12}\equiv{2}\ \text{ mod }\ {5}\right)}$

What is ${e}^{{-{1}}}$ ?

One might expect this to be ${e}^{{-{1}}}={\left(\frac{{1}}{{e}}\right)}^{{1}}$, but we're only dealing with integers here and not rationals, so what could it be?

According to RSA the following should be true:

${m}\equiv{c}^{{d}}\ \text{ mod }\ {N}$

${m}\equiv{\left({m}^{{e}}\ \text{ mod }\ {N}\right)}^{{d}}\ \text{ mod }\ {N}$

${m}\equiv{m}^{{{e}\cdot{d}}}\ \text{ mod }\ {N}$

${m}\equiv{m}^{{1}}\ \text{ mod }\ {N}$

${m}\equiv{m}\ \text{ mod }\ {N}$

The public exponent ${e}$ and the private exponent ${d}$ are cancelling each other out, making them "inverse" to each other. So in modular arithmetic ${e}^{{-{1}}}$ is the "modular multiplicative inverse" of ${e}$.

${e}\cdot{d}\equiv{e}\cdot{e}^{{-{1}}}\equiv{1}\ \text{ mod }\ \phi{\left({N}\right)}$

Knowing that, we can also see why the notiation of ${e}^{{-{1}}}$ was chosen to represent the inverse when we go back to using rational numbers:

${e}\cdot{d}={e}\cdot{e}^{{-{1}}}={e}\cdot{\left(\frac{{1}}{{e}}\right)}^{{1}}={1}$

Why does inversion work?

At first it looks quite simple: We just have to find two integers ${e}$ and ${d}$ such that when multiplied with each other they result in 1 (within $\text{mod }\ {n}$) and are therefore inverse to each other:

${e}\cdot{d}\equiv{1}\ \text{ mod }\ {n}$

An interesting aspect to this is, that it only has solutions when ${e}$ and ${d}$ are "coprime" (or "relatively prime") to ${n}$. Meaning that the greatest common divisior, the biggest integer that divides both numbers without a remainder, is 1.

${\gcd{{\left({e},{n}\right)}}}={1}$ and ${\gcd{{\left({d},{n}\right)}}}={1}$

Example

Let's look for the inverse ${d}$ of 5 within ${\left(\text{mod }\ {15}\right)}$:

${5}\cdot{d}\equiv{1}\ \text{ mod }\ {15}$

With ${\gcd{{\left({5},{15}\right)}}}={5}$ there should not be a solution for ${\left({\left({d}\cdot{5}\right)}\ \text{ mod }\ {15}\right)}={1}$, is that true?

|              d |  0 |  1 |  2 |  3 |  4 |  5 |  6 |   ...    |
|----------------|----|----|----|----|----|----|----|----------|
| ((d⋅5) mod 15) |  0 |  5 | 10 |  0 |  5 | 10 |  0 | {0,5,10} |

The numbers this can yield quickly start to repeat and none of them are 1, so there is indeed no inverse.

Okay, but 15 is a multiple of 5 so the result is not that much of a surprise.

What about 6?

${6}\cdot{d}\equiv{1}\ \text{ mod }\ {15}$

With ${\gcd{{\left({6},{15}\right)}}}={3}$ there should still not be a solution for ${\left({\left({d}\cdot{6}\right)}\ \text{ mod }\ {15}\right)}={1}$, but this time 15 is clearly not a multiple of 6 so what happens now?

|              d |  0 |  1 |  2 |  3 |  4 |  5 |  6 |     ...      |
|----------------|----|----|----|----|----|----|----|--------------|
| ((d⋅6) mod 15) |  0 |  6 | 12 |  3 |  9 |  0 |  6 | {0,3,6,9,12} |

Still no inverse, but something interesting becomes visible: The numbers yielded are always multiples of ${\gcd{{\left({e},{n}\right)}}}$.

Let's try a number which should actually have an inverse: ${\gcd{{\left({8},{15}\right)}}}={1}$. It may be worth pointing out here that neither numbers are prime, but with this result they are still "relative prime" to each other.

|              d |  0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |  8 |  9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |                ...                   |
|----------------|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|--------------------------------------|
| ((d⋅8) mod 15) |  0 |  8 |  1 |  9 |  2 | 10 |  3 | 11 |  4 | 12 |  5 | 13 |  6 | 14 |  7 |  0 |  8 |  1 | {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14} |

Not only has 8 an inverse but the numbers yielded are also all numbers from 0 to 14. Thanks to the greatest common divisor being 1, the resulting numbers are multiples of 1 as well. This time it is as if there's a 1-to-1 mapping between ${d}$ and the resulting numbers as long as ${d}\lt{n}$.

Why does an inverse from $\text{mod }\ \phi{\left({N}\right)}$ still seem to work in $\text{mod }\ {N}$ ?

We've seen that the inverse of an integer depends on the modulo. The inverse for 8 in ${\left(\text{mod }\ {15}\right)}$ is 2. But in ${\left(\text{mod }\ {13}\right)}$ it would be 5.

In RSA ${d}$ is calculated as the inverse of ${e}$ in $\text{mod }\ \phi{\left({N}\right)}$:

${d}\equiv{e}^{{-{1}}}\ \text{ mod }\ \phi{\left({N}\right)}$ and therefore ${e}\cdot{d}\equiv{1}\ \text{ mod }\ \phi{\left({N}\right)}$

But during decryption ${d}$ and ${e}$ appear to be cancelling each other out even under ${\left(\text{mod }\ {N}\right)}$, why does that work?

${m}\equiv{m}^{{{e}\cdot{d}}}\equiv{m}^{{1}}\ \text{ mod }\ {N}$

Unfortunately there doesn't seem to be a good way to explain this without making use of (a little bit of magic called) Euler's Totient Theorem which shows that for an integer ${a}$ that is coprime with ${n}$ the following applies:

${a}^{{\phi{\left({n}\right)}}}\equiv{1}\ \text{ mod }\ {n}$

To make use of that we have to look for a $\phi{\left({N}\right)}$ in the message's exponent and we can quite easily find it:

${e}\cdot{d}\equiv{1}\ \text{ mod }\ \phi{\left({N}\right)}\Rightarrow{e}\cdot{d}={1}+{k}\cdot\phi{\left({N}\right)}$ with the integer ${k}\ge{0}$

$\Rightarrow{m}\equiv{m}^{{{e}\cdot{d}}}\equiv{m}^{{{1}+{k}\cdot\phi{\left({N}\right)}}}\equiv{m}^{{1}}\cdot{m}^{{\phi{\left({N}\right)}\cdot{k}}}\equiv{m}\cdot{\left({m}^{{\phi{\left({N}\right)}}}\right)}^{{{k}}}\equiv{m}\cdot{1}^{{k}}\ \text{ mod }\ {N}$

Thanks to Euler's Theorem it seems like we can remove everything except for message ${m}$ from the formula with ${\left({m}^{{\phi{\left({N}\right)}}}\equiv{1}\ \text{ mod }\ {N}\right)}$.

But you might remember I mentioned the Theorem should only apply when ${m}$ is coprime with ${N}$, which would restrict the valid messages we would be able to encrypt. If ${N}$ was a prime that would not be an issue as all integers ${\left({1}\le{m}\lt{N}\right)}$ would be relatively prime to it.

Why does Euler's Theorem still seem to apply for ${\gcd{{\left({m},{N}\right)}}}\ne{1}$?

First, note that because both ${p}$ and ${q}$ are prime their greatest common divisor is always 1. If ${m}$ is not coprime with ${N}$ that must mean that it is a multiple of either ${p}$ or ${q}$, meaning it can't be coprime with one of them. But it must be coprime with at least one of them, because in order to not be coprime with both of them it must be a multiple of both ${p}$ and ${q}$ and that cannot be the case as long as ${m}\lt{N}$ since ${N}$ is the first possible number to be a multiple of both: ${N}={p}\cdot{q}$.

Therefore even when ${\gcd{{\left({m},{N}\right)}}}\ne{1}$ either ${p}$ or ${q}$ will share a residue of 0 with the message (since ${m}$ would be a multiple of it without leaving a remainder) and the other one would be either:

${\left({g}{d}{c}{\left({m},{p}\right)}={1}\right)}\Rightarrow{\left({m}\cdot{m}^{{\phi{\left({N}\right)}}}\equiv{m}\cdot{m}^{{\phi{\left({p}\right)}\cdot\phi{\left({q}\right)}}}\equiv{m}\cdot{\left({m}^{{\phi{\left({p}\right)}}}\right)}^{{\phi{\left({q}\right)}}}\equiv{m}\cdot{1}^{{\phi{\left({q}\right)}}}\equiv{m}\cdot{1}\ \text{ mod }\ {p}\right)}$

or

${\left({g}{d}{c}{\left({m},{q}\right)}={1}\right)}\Rightarrow{\left({m}\cdot{m}^{{\phi{\left({N}\right)}}}\equiv{m}\cdot{m}^{{\phi{\left({p}\right)}\cdot\phi{\left({q}\right)}}}\equiv{m}\cdot{\left({m}^{{\phi{\left({q}\right)}}}\right)}^{{\phi{\left({p}\right)}}}\equiv{m}\cdot{1}^{{\phi{\left({p}\right)}}}\equiv{m}\cdot{1}\ \text{ mod }\ {q}\right)}$

With these, we have either one of the following systems of congruence:

${\left({m}\equiv{m}\ \text{ mod }\ {p}\right)}$, ${\left({m}\equiv{0}\ \text{ mod }\ {q}\right)}$

or

${\left({m}\equiv{0}\ \text{ mod }\ {p}\right)}$, ${\left({m}\equiv{m}\ \text{ mod }\ {q}\right)}$

Both of which can be simplified using the Chinese Remainder Theorem to:

${\left({m}\equiv{m}\ \text{ mod }\ {p}\cdot{q}\right)}$

Example

${p}={7},{q}={11}$

${N}={p}\cdot{q}\ ={7}\cdot{11}={77}$

$\phi{\left({N}\right)}=\phi{\left({p}\right)}\cdot\phi{\left({q}\right)}={\left({p}-{1}\right)}\cdot{\left({q}-{1}\right)}={\left({7}-{1}\right)}\cdot{\left({11}-{1}\right)}={60}$

${e}={7}$

${d}\equiv{e}^{{-{1}}}\ \text{ mod }\ \phi{\left({N}\right)}={43}\ \text{ mod }\ {60}$ with ${7}\cdot{43}\equiv{1}\ \text{ mod }\ {60}$

${c}\equiv{m}^{{e}}\ \text{ mod }\ {N}\equiv{42}^{{7}}\ \text{ mod }\ {77}={70}$ with ${\gcd{{\left({m},{N}\right)}}}={\gcd{{\left({42},{60}\right)}}}={6}$

${m}\equiv{c}^{{d}}\ \text{ mod }\ {N}\equiv{70}^{{43}}\ \text{ mod }\ {77}\equiv{42}$

Despite ${m}$ not being coprime with ${N}$ thanks to:

${\gcd{{\left({m},{p}\right)}}}={\gcd{{\left({42},{7}\right)}}}={7}$ therefore ${m}\equiv{m}\ \text{ mod }\ {p}\equiv{42}\ \text{ mod }\ {7}\equiv{0}\ \text{ mod }\ {7}$

${\gcd{{\left({m},{q}\right)}}}={\gcd{{\left({42},{11}\right)}}}={1}$ therefore ${m}\equiv{m}^{{{e}{d}}}\equiv{m}^{{{1}+{k}\cdot\phi{\left({q}\right)}}}\equiv{m}^{{1}}\cdot{\left({m}^{{\phi{\left({q}\right)}}}\right)}^{{k}}\equiv{m}\cdot{1}^{{k}}\ \text{ mod }\ {q}\equiv{42}\ \text{ mod }\ {11}$

Therefore ${m}\equiv{m}\ \text{ mod }\ {p}\cdot{q}\equiv{42}\ \text{ mod }\ {\left({7}\cdot{11}\right)}$

Why does Euler's Theorem work?

First of all, Euler's Totient Theorem is a generalization of Fermat's Little Theorem where for a prime ${p}$ for any integer ${a}$ the following is true:

${\left({a}^{{p}}\equiv{a}\ \text{ mod }\ {p}\right)}\Leftrightarrow{\left({a}^{{p}}-{a}\equiv{0}\ \text{ mod }\ {p}\right)}$

Next, we need to look at Euler's function, denoted as $\phi{\left({n}\right)}$. This function counts the number of positive integers up to ${n}$ that are relatively prime to ${n}$. In other words, it counts the number of integers that have a greatest common divisor of 1 with ${n}$. When ${n}$ is a prime number ${p}$, all the numbers from ${1}$ to ${\left({p}-{1}\right)}$ are relatively prime to ${p}$, so $\phi{\left({p}\right)}={p}-{1}$.

Euler's Theorem generalizes Fermat's Little Theorem and states that for any positive integer ${n}$ and any integer ${a}$ relatively prime to ${n}$, we have:

${\left({a}^{\phi}{\left({n}\right)}\right)}\equiv{1}{\left(\text{mod }\ {n}\right)}$

Which is in case for ${n}={p}$ prime equivalent to:

${\left({a}^{{{p}-{1}}}\right)}\equiv{1}{\left(\text{mod }\ {p}\right)}$

Example

A very simple way to gain some intution for these Theorems is through, what one might call, a modulo-lookup-table:

|    0 |    1 |    2 |    3 |    4 |
|------|------|------|------|------|
|    5 |    6 |    7 |    8 |    9 |
|   10 |   11 |   12 |   13 |   14 |
|   15 |   16 |   17 |   18 |   19 |
|   20 |   21 |   22 |   23 |   24 |
|   25 |   26 |   27 |   28 |   29 |
|   30 |   31 |   32 |   33 |   34 |
:      :      :      :      :      :
|   80 |   81 |   82 |   83 |   84 |
:      :      :      :      :      :
|  240 |  241 |  242 |  243 |  244 |
|  245 |  246 |  247 |  248 |  249 |
|  250 |  251 |  252 |  253 |  254 |
|  255 |  256 |  257 |  258 |  259 |
:      :      :      :      :      :
| 1020 | 1021 | 1022 | 1023 | 1024 |
:      :      :      :      :      :

Imagine this (modulo 5) lookup-table just continues to infinity and always tells us at what remainder we would end up with if we applied ${\left(\text{mod}{5}\right)}$.

Now let's check ${\left({a}^{{p}}\equiv{a}\ \text{ mod }\ {p}\right)}$:

0**5 mod 5 =    0 mod 5
1**5 mod 5 =    1 mod 5
2**5 mod 5 =   32 mod 5
3**5 mod 5 =  243 mod 5
4**5 mod 5 = 1024 mod 5

With the help of the lookup-table we can easily determine the remainder of the division by checking in which column we find the number. The Theorem works.

Although it's mathematically equivalent, let's check ${\left({a}^{{p}}-{a}\equiv{0}\ \text{ mod }\ {p}\right)}$ too:

0**5 mod 5 = (   0 - 0) mod 5 =    0 mod 5
1**5 mod 5 = (   1 - 1) mod 5 =    0 mod 5
2**5 mod 5 = (  32 - 2) mod 5 =   30 mod 5
3**5 mod 5 = ( 243 - 3) mod 5 =  240 mod 5
4**5 mod 5 = (1024 - 4) mod 5 = 1020 mod 5

Here we can see that we always end up in the 0-column, just as we should.

Finally, let's look at ${a}^{{{p}-{1}}}\equiv{1}\ \text{ mod }\ {p}$:

0**4 mod 5 =    0 mod 5
1**4 mod 5 =    1 mod 5
2**4 mod 5 =   16 mod 5
3**4 mod 5 =   81 mod 5
4**4 mod 5 =  256 mod 5

Since 0 can't have a greatest common divisor with anything, it also can't be coprime so it yields 0 instead of 1. But as long as the base is coprime to the modulo we always end up in the 1-column.

What is the Chinese Remainder Theorem?

The last trick to explain is why the Chinese Remainder Theorem shows that ${\left({m}\equiv{m}\cdot{m}^{{\phi{\left({N}\right)}}}\ \text{ mod }\ {p}\cdot{q}\right)}\Rightarrow{\left({m}\equiv{m}\cdot{1}\ \text{ mod }\ {p}\cdot{q}\right)}$ despite ${m}$ not being coprime to both ${p}$ and ${q}$.

The Chinese Remainder Theorem (CRT) allows us to solve a system of linear congruences with pairwise coprime moduli. It states that if you have a system of linear congruences like:

x ≡ a1 (mod n1)
x ≡ a2 (mod n2)
...
x ≡ ak (mod nk)

where ${n}{1},{n}{2},\ldots,{n}{k}$ are pairwise coprime (i.e., they share no common factors other than 1), then there exists a unique solution for ${x}$ modulo the product of the moduli, i.e., modulo ${N}={n}{1}\cdot{n}{2}\cdot$ ... $\cdot{n}{k}$:

${x}\equiv{\left({a}_{{1}}\cdot\frac{{N}}{{{n}_{{1}}}}\cdot{\left({\left(\frac{{N}}{{{n}_{{1}}}}\right)}^{{-{1}}}\ \text{ mod }\ {n}_{{1}}\right)}\right)}+{\left({a}_{{2}}\cdot\frac{{N}}{{{n}_{{2}}}}\cdot{\left({\left(\frac{{N}}{{{n}_{{2}}}}\right)}^{{-{1}}}\ \text{ mod }\ {n}_{{2}}\right)}\right)}+$ ... $+{\left({a}_{{k}}\cdot\frac{{N}}{{{n}_{{k}}}}\cdot{\left({\left(\frac{{N}}{{{n}_{{k}}}}\right)}^{{-{1}}}\ \text{ mod }\ {n}_{{k}}\right)}\right)}{\left(\text{mod }\ {N}\right)}$

In the context of RSA, we have ${N}={p}\cdot{q}$ where ${p}$ and ${q}$ are distinct prime numbers, and thus, they are coprime.

m ≡ m (mod p)
m ≡ m (mod q)

Example

Based on the systems of congruence from the previous RSA calculation example:

${m}\equiv{m}\ \text{ mod }\ {p}\equiv{42}\ \text{ mod }\ {7}\equiv{0}\ \text{ mod }\ {7}$

${m}\equiv{m}^{{{e}{d}}}\equiv{m}^{{{1}+{k}\cdot\phi{\left({q}\right)}}}\equiv{m}^{{1}}\cdot{\left({m}^{{\phi{\left({q}\right)}}}\right)}^{{k}}\equiv{m}\cdot{1}^{{k}}\ \text{ mod }\ {q}\equiv{42}\ \text{ mod }\ {11}$

We now use the CRT step by step:

${m}={\left({\left({m}\ \text{ mod }\ {p}\right)}\cdot\frac{{{p}\cdot{q}}}{{p}}\cdot{\left({\left(\frac{{{p}\cdot{q}}}{{p}}\right)}^{{-{1}}}\ \text{ mod }\ {p}\right)}\right)}+{\left({\left({m}\ \text{ mod }\ {q}\right)}\cdot\frac{{{p}\cdot{q}}}{{q}}\cdot{\left({\left(\frac{{{p}\cdot{q}}}{{q}}\right)}^{{-{1}}}\ \text{ mod }\ {p}\right)}\right)}{\left(\text{mod }\ {p}\cdot{q}\right)}$

${m}={\left({\left({m}\ \text{ mod }\ {p}\right)}\cdot{q}\cdot{\left({q}^{{-{1}}}\ \text{ mod }\ {p}\right)}\right)}+{\left({\left({m}\ \text{ mod }\ {q}\right)}\cdot{p}\cdot{\left({p}^{{-{1}}}\ \text{ mod }\ {q}\right)}\right)}{\left(\text{mod }\ {p}\cdot{q}\right)}$

${m}={\left({\left({0}\ \text{ mod }\ {p}\right)}\cdot{11}\cdot{\left({11}^{{-{1}}}\ \text{ mod }\ {7}\right)}\right)}+{\left({\left({42}\ \text{ mod }\ {q}\right)}\cdot{7}\cdot{\left({7}^{{-{1}}}\ \text{ mod }\ {11}\right)}\right)}{\left(\text{mod }\ {7}\cdot{11}\right)}$

${m}={\left({0}\cdot{11}\cdot{2}\right)}+{\left({9}\cdot{7}\cdot{8}\right)}{\left(\text{mod }\ {77}\right)}$

${m}={504}{\left(\text{mod }\ {77}\right)}={42}$